Tema 7. Teoría de la probabilidad.

Probabilidad: se usa con sucesos inciertos, suele ser expresado en porcentajes o

con valores entre 0-1. Se suele emplear para la toma de decisiones.

-Enfoque clásico/ a priori: es el cociente entre el número de casos favorables de aparición

entre el número total de casos posibles. Hay eventos que tienen el mismo porcentaje de aparición que en la posteriori. Es un enfoque objetivo. Su fórmula es P(E)=M/N, siendo P la probabilidad, E la característica, M el número de veces que E se repite y N el número total de veces que se intenta. Cuanto más repitamos el experimento más se estabiliza el resultado.

-A posteriori: para ésta el suceso se repite un número M de veces, siendo ésta la

probabilidad de ocurrencia de E. Su fórmula es la misma que a priori. Si N es un número excesivamente grande se puede calcular con límites.

 

Casos y sucesos: el conjunto de todos los datos obtenidos del experimento 

conforman el llamado "espacio muestral" (S). Un suceso complementario es aquel que aparece cuando no se da otro. Puede existir eventos que no sean excluyentes por lo que se puede ser partícipe de más de un subconjunto. Se unen el totales de datos de la categoría A y el total de la categoría B, a ésto se le denominaría AUB (unión de A y B). En la intersección, no se suma el total de A y el total de B, se toman los datos de aquellos que pertenezcan a ambos subconjuntos exclusivamente.

Propiedades de las probabilidades: 

-Dos sucesos excluyentes: si queremos saber AUB, probabilidad de que se de el suceso A

y el suceso B, sólo habría que sumarlas.  Su fórmula es P(AUB)= P(A)+P(B).

-Dos sucesos no excluyentes: si queremos saber la probabilidad de que se produzca A y B

habría que sumar la probabilidad de aparición de A con la de B, restando a aquellos que posean ambas características. Su fórmula es P(AUB)= P(A)+P(B)-P(AՈB).

 -Dos sucesos que son independientes: que uno ocurra no influye en que otro aparezca. 

Su fórmula es P(AՈB)= P(A)*P(B). 

Reglas básicas (teoría de la probabilidad):  la

probabilidad de que es suceso ocurra va entre 0 (jamás ocurre) y 1 (siempre ocurre). La probabilidad de que el suceso A repercuta sobre el B se calcula P(A/B)= P(AՈB)/P(B). Si repercute es a priori. 

Teorema de bases: vincula la probabilidad condicional de que A ocurra,

cuando B (probabilidad condicionada) se da y viceversa. Su fórmula es 

P(A/B)= (P(B/A)*P(A)) / (P(B/A)*P(A)+P(B/A')*P(A')).

Distribución de probabilidad en variables 

discretas: 

-Distribución binominal: se usa cuando sólo existen 2 opciones y el resultado anterior no

repercute sobre el siguiente. Al suceso A se le representa por p, el suceso B es equivalente a 1-p y se le representa por q. El experimento se repetirá un número N de veces.

-Distribución de Poisson: se llama también distribución de casos raros. A partir de una 

probabilidad media, se calcula el número de veces que un suceso, que presenta un porcentaje de aparición muy bajo, puede darse en un periodo de tiempo determinado. 

 

 

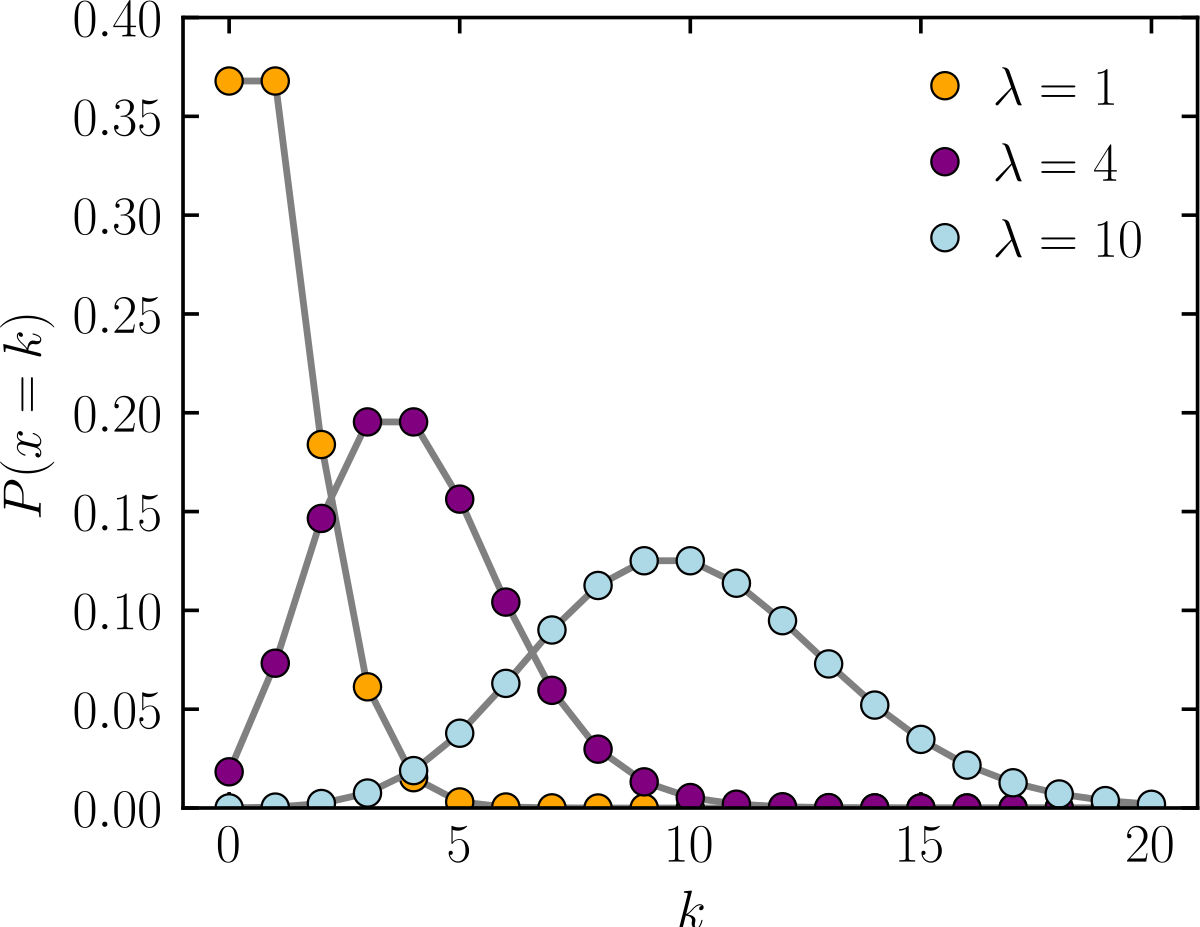
  Distribución de Poisson.

Distribución normal: Gauss comprobó que en el punto más alto de la

gráfica coinciden la media, la moda y la mediana. También se dio cuenta de que si a la mediana le sumas y le restas el valor de una desviación típica se obtiene un valor de 68,26%, si se suman 2 desviaciones típicas se obtiene 95,45%, y que si sumo y resto 3 desviaciones típicas obtengo 99,73%.

 

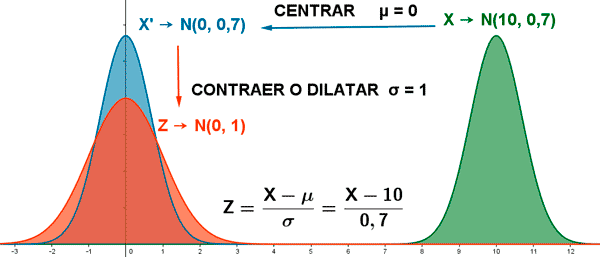
Tripificación de valores de una normal: 

Extrapolando aparecen principios básicos de las distribuciones normales y así podemos tripificar valores de una normal. Tripicar consiste en convertir los valores de una normal a valores de una normal estándar. Se puede hacer si se trabajan con variables contínuas que presenten más de 100 unidades.